背包九讲

秃头王

发布于：2021年3月7日

动态规划

动态规划（Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。动态规划往往用于优化递归问题，例如斐波那契数列，如果运用递归的方式来求解会重复计算很多相同的子问题，利用动态规划的思想可以减少计算量。通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，具有天然剪枝的功能，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

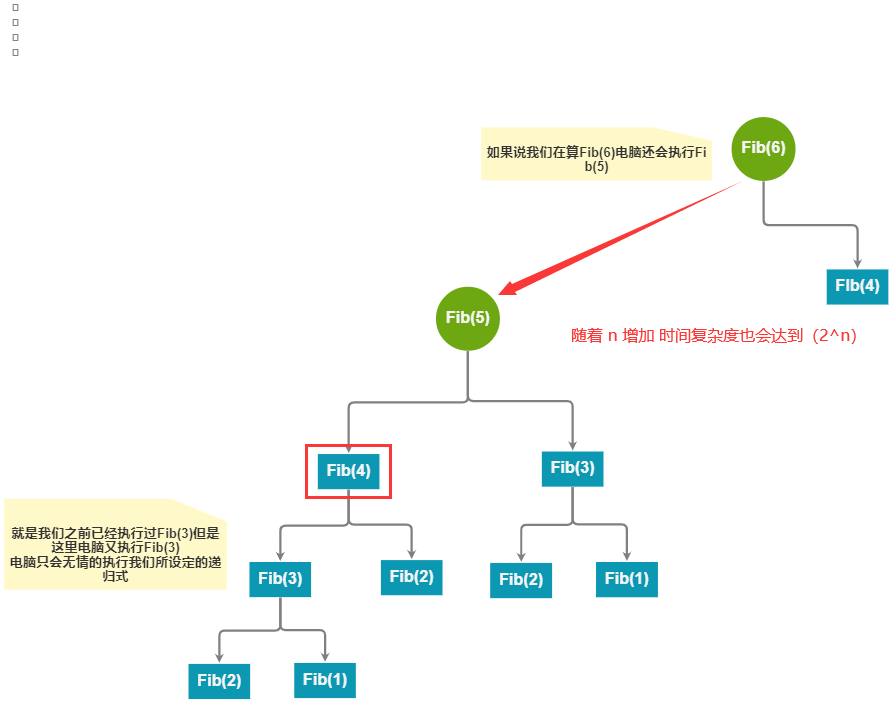
在大家看完什么是动态规划后就是说我们在之前也做题中可能也遇到过动态规划的题比如斐波那契数列 如 1，1， 2， 3… 就是这个 2 怎么来的就是 1 + 1 = 2 之后 3 的下一项是什么？就是 2 + 3 = 5 也就是说 3 的下一项就是 5 之后下几项就是 8，13，21…就会得到这组序列我们如果相求第n斐波那契数列可以得到转移公式 $Fib(n) = Fib(n - 1) + Fib(n - 2);$ (Fib(1) = 1 和 Fib(2) = 1是由题目给出的，n > 2 ) 完整的斐波那契数列加上出口就是 n = 1 or n = 2 返回 1 , 就是说我们这里为什么提出这个斐波那契数列呢就是我们在递归时候，我们呢会发现他的递归式中会出现重叠的子问题，为什么会这么说我来计算一下斐波那契数列第 5 项 Fib(5) 可得出如下

假如说我们用数组去求解Fib(6) 是不就可以直接用之前求Fib(5) + Fib(4) 的直接得到 Fib(6) 这样我是不是就可以省去求重叠子问题的时间，这样我们的时间复杂度就从o(2^n^) 变成 o(n)(当然这个时间复杂度也是能弄记忆化搜索优化的)。

例题

01 背包只又 2 种选择一种选一种不选。洛谷 P1048 采药

完全背包每件物品可以无限选（只要不超过背包的总体积）。洛谷 P1616 疯狂的采药

多重背包每个物品有相应的个数。洛谷 P1776 宝物筛选

混合背包基于以上上面三种背包。洛谷 P1833 樱花

二维费用背包类比以一维费用01背包，推广二维费用01背包。洛谷 P1507 NASA的食物计划

分组背包有 n 组物品每组物品有若干个，同一组内互相冲突，同一组最多只能选一个或者不选洛谷 P1757 通天之分组背包

有依赖的背包类似捆绑销售买附必须买主，买主可以不买附洛谷 P1064 金明的预算方案

背包九讲

0-1背包

题目：

有一天小鲁同学在家里学习算法，小鲁的妈妈就叫这个铲屎官小鲁去收拾一下，但是小鲁很不想去就说我在学习算法，小鲁的妈妈就说你要是在不去我就把你一起也铲出去，小鲁就想被你铲除去还不如我自己走，这样小鲁就回到了自己的房间，打破了储存已久的小猪储存罐🐖。

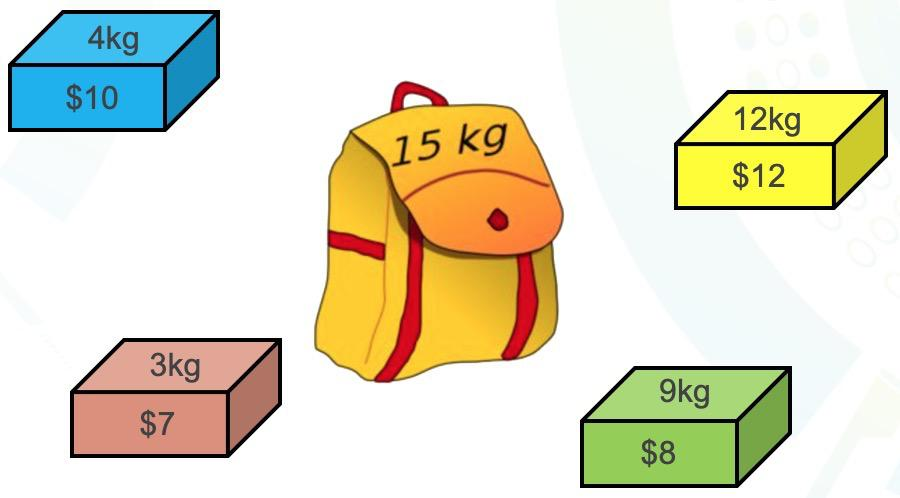
小鲁的背包可容纳下总重量为 20（ s ）他需要带尽可能多的钱走。（没种钱可以重复的选取没有上限）。

简单的说：

有N件物品和一个容量为T的背包。第i件物品的费用是t[i]，价值是v[i]。求解将哪些物品装入背包可使价值总和最大。

下标	重量（w）	价值（v）
1	2	3
2	3	4
3	4	5
4	5	8
5	9	10

这里为什么不用贪心而用动态规划？

首先贪心他是局部最优解，而我所讲的动态规划可以达到全局最优解。

基本思路：

首先我们考虑什么，取不取第 n 件物品？

取 $-> n - 1$ 个物品，背包大小 $s - w[n]$

不取$ -> n - 1$ 个物品，背包大小 s
1. 定义状态：$dp[i][j]$ 表示考虑前 i 个物品，背包大小 $0 -> j $, 获得最大价值。
2. 转移方程：$dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])$

代码实现：

无优化-代码

#include<iostream>
using namespace std;

#define MAX_N 1000

int dp[MAX_N + 10][MAX_N + 10];
int t[MAX_N + 10], v[MAX_N + 10];

void backpack(int k, int T) {
    for (int i = 1; i <= k; i++) {
        for (int j = 1; j <= T; j++) {
            if (t[i] > j) {
                dp[i][j] = dp[i - 1][j];
            } else {
                int Y = dp[i - 1][j - t[i]] + v[i];
                int T = dp[i - 1][j];
                dp[i][j] = Y > T ? Y : T;
                // dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
            }
        }
    }
}

int main() {
    int T, n;
    cin >> T >> n;
    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> v[i];
    }
    backpack(n, T);
    cout << dp[n][T];
}

#include <iostream>
using namespace std;

const int MAX_N = 1e3;

int n, m;
int f[MAX_N + 10][MAX_N + 10], w[MAX_N + 10], v[MAX_N + 10];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= m; i++) {
        cin >> w[i] >> v[i];
    }

    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            f[i][j] = f[i - 1][j];
            if(j >= w[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
        }
    }
    cout << f[m][n] << endl;
    return 0;
}

优化-代码

#include <iostream>
#include <cmath>
using namespace std;

#define MAX_N 1000

int dp[MAX_N];
int T[MAX_N], V[MAX_N];

void backpack(int k, int s) {
    for (int i = 1; i <= k; i++) {
        for (int j = s; j >= T[i]; j--) {
            dp[j] = max(dp[j], dp[j - T[i]] + V[i]);
        }
    }
    return ;
}

int main() {
    int t, n;
    cin >> t >> n;
    for (int i = 1; i <= n; i++) {
        cin >> T[i] >> V[i];
    }
    backpack(n, t);
    cout << dp[t];
    return 0;
}

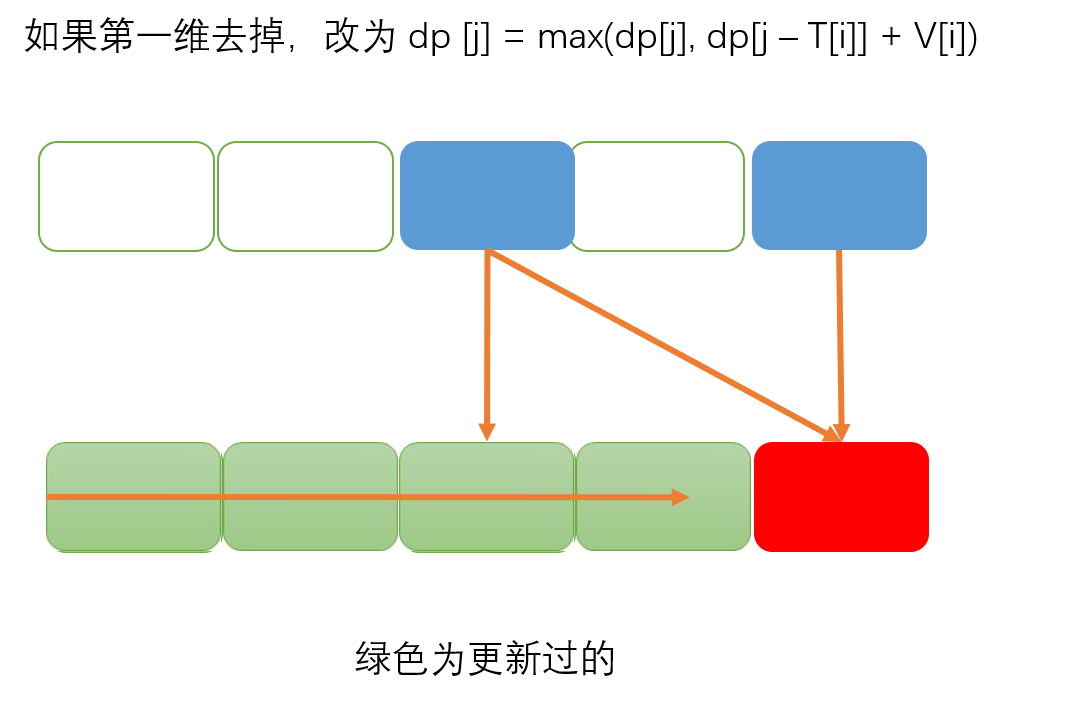
上面朴素算法时间复杂度与空间复杂度皆为 O(t*n) 其中时间复杂度不能再优化, 而空间复杂度可以优化为O(t), 下面我们来讲解如何优化到一维数组

细节问题

1 我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。
如果是第一种问法，要求恰好装满背包，那么在初始化时除了f[0]为0其它f[1..V]均设为-∞，这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。

2 如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将f[0..V]全部设为0。为什么呢？

3 可以这样理解：初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可能被价值为0的（相当于没装东西），其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。
这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状态转移之前的初始化进行讲解。

完全背包

题目：

有N种物品和一个容量为T的背包，每种物品都有无限件可用。第i种物品的费用是t[i]，价值是v[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

基本思路：

和 01背包很相似转移方程相同

转移方程：$dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])$

与 01背包的区别–第二个循环

01背包在更新时候倒序因为是需要用之前元素

代码实现：

无优化-代码

#include<iostream>
using namespace std;

const int MAX_N = 1e4;

long long dp[MAX_N + 10][MAX_N +10];
long long t[MAX_N + 10], v[MAX_N + 10];

void backpack(int k, int s) {
    for (int i = 1; i <= k; i++) {
        for (int j = 1; j <= s; j++) {
            if (j < t[i]) dp[i][j] = dp[i - 1][j];
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - t[i]] + v[i]);
            }
        }
    }
    return ;
}

int main() {
    int T, n;
    cin >> T >> n;
    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> v[i];
    }
    backpack(n, T);
    cout << dp[n][T] << endl;
    return 0;
}

优化-代码

#include<iostream>
using namespace std;

const int MAX_N = 1e7;

long long B[MAX_N + 10];
int t[MAX_N + 10], v[MAX_N + 10];

void backpack(int k, int s) {
    for (int i = 1; i <= k; i++) {
        for (int j = t[i]; j <= s; j++) {
            B[j] = max(B[j], B[j - t[i]] + v[i]);
        }
    }
    return ;
}

int main() {
    int T, n;
    cin >> T >> n;
    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> v[i];
    }
    backpack(n, T);
    cout << B[T] << endl;
    return 0;
}

多重背包

题目：

有N种物品和一个容量为s的背包。第i种物品最多有m[i]件可用，每件费用是w[i]，价值是v[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

基本思路：

这题目和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改即可，因为对于第i种物品有m[i]+1种策略：取0件，取1件……取n[i]件。令f[i][j]表示前i种物品恰放入一个容量为v的背包的最大权值。

则转移方程：

$dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * w] + k * v);$

代码实现：

无优化-代码

// 多重背包 朴素 算法

#include<iostream>
using namespace std;

const int MAX_N = 1e3;

int dp[MAX_N + 10][MAX_N + 10];

int main() {
    int n, s;
    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        // 价值  重量  组数
        int v, w, m;
        cin >> v >> w >> m;
        for (int j = s; j >= w; j--) { // 背包容量
            for (int k = 0; k <= m && j >= k * w; k++) { // 决策
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * w] + k * v);
            }
        }
    }
    cout << dp[n][s] << endl;
    return 0;
}

转化为01背包问题

另一种好想好写的基本方法是转化为01背包求解：把第i种物品换成log(m)件01背包中的物品.

但是我们期望将它转化为01背包问题之后能够像完全背包一样降低复杂度。仍然考虑二进制的思想.

二进制优化

假设有50个苹果，现在要取n个苹果(n≤50），如何取?朴素的做法应该是将苹果一个一个拿出来，直到n个苹果被取出来。
再假设有50个苹果和6只箱子，利用箱子进行某些预备工作，可以在每个箱子中放2(k≥0)个苹果，也就是1、2、4、8、16、19（剩余的数），取任意n个苹果时，只要推出忆只箱子就可以了。

lg45÷lg2=1.6532125÷0.301029996=5.49185

优化-代码


#include<iostream>
using namespace std;

const int MAX_N = 1e5;

int dp[MAX_N + 10];
int ww[MAX_N + 10], vv[MAX_N + 10], mm[MAX_N + 10];

int main () {
    int n, s, count = 1, v, w, m;
    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        cin >> v >> w >> m;
        for (int j = 1; j <= m; j <<= 1) {
            ww[count] = j * w;
            vv[count++] = j * v;
            m -= j;
        }
        // 处理 二进制拆分不了的
        if (m) {
            ww[count] = m * w;
            vv[count++] = m * v;
        }
    }

    // 01 背包 模板
    for (int i = 1; i < count; i++) {
        for (int j = s; j >= ww[i]; j--) {
            dp[j] = max(dp[j], dp[j - ww[i]] + vv[i]);
        }
    }
    cout << dp[s] << endl;
    return 0;
}

混合背包

题目：

如果将 01背包、完全背包、多重背包、混合起来。也就是说，有的物品只可以取一次（01背包），有的物品可以取无限次（完全背包），有的物品可以取的次数有一个上限（多重背1包）。应该怎么求解呢？

基本思路：

01背包与完全背包的混合

我只需要考虑到在01背包和完全背包中给出的代码只有一处不同，故如果只有两类物品：一类物品只能取一次，另一类物品可以取无限次，那么只需在对每个物品应用转移方程时，根据物品的类别选用顺序或逆序的循环即可.

if // 如果是 01 背包
	for (int j = s; j >= w[i] j--) {
    	dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
	}
else // 如果是 完全背包
    for (int j = w[i]; j <= s; j++) {
        dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    }

再加上多重背包

如果再加上有的物品最多可以取有限次，我们就可以用二进制拆分来把多重背包转换成01背包

// m = 物品最多能取的个数
for (int j = 1; j <= m; j <<= 1) {
    ww[count] = j * w;
    vv[count++] = j * v;
     m -= j;
}
// 处理 二进制拆分不了的
if (m) {
	ww[count] = m * w;
	vv[count++] = m * v;
}

题解-代码：


#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;

const int MAX_N = 1e5;

int dp[MAX_N + 10], ww[MAX_N + 10], vv[MAX_N + 10], mark[MAX_N + 10];

int main() {
    int T, t1, t11, t2, t22, n, count = 1;
    scanf("%d:%d %d:%d %d", &t1, &t11, &t2, &t22, &n);
    T = (t2 * 60 + t22) - (t1 * 60 + t11);
    for (int i = 1; i <= n; i++) {
        int w, v, m;
        cin >> w >> v >> m;
        if (!m) {
            ww[count] = w;
            vv[count] = v;
            // 标记为 0 代表可以重复观看  完全背包
            mark[count++] = 0;
        } else {
            // 二进制拆分转换 01背包
            for (int j = 1; j <= m; j <<= 1) {
                ww[count] = j * w;
                vv[count] = j * v;
                // 标记为 1 代表每棵树只能看或者不看  01背包
                mark[count++] = 1;
                m -= j;
            }
            // 因为二进制拆分 只能是 1 2 4 8 16 32 比如 m = 10 二进制拆分之后还会余下 1 下面 if 就是解决那个多余出来的
            if (m) {
                ww[count] = m * w;
                vv[count] = m * v;
                mark[count++] = 1;
            }
        }
    }
    // 实现 01背包 和 完全背包 模板就行了
    for (int i = 1; i < count; i++) {
        if (mark[i]) {
            // 如果 mark[i] == 1 就执行 01背包
            for (int j = T; j >= ww[i]; j--) {
                dp[j] = max(dp[j], dp[j - ww[i]] + vv[i]);
            }
        } else {
            for (int j = ww[i]; j <= T; j++) {
                dp[j] = max(dp[j], dp[j - ww[i]] + vv[i]);
            }
        }
    }
    cout << dp[T] << endl;
    return 0;
}

二维费用背包

题目：

二维费用的背包问题是指：对于每件物品，具有两种不同的费用；选择这件物品必须同时付出这两种代价；对于每种代价都有一个可付出的最大值（背包容量）。问怎样选择物品可以得到最大的价值。设这两种代价分别为代价1和代价2，第i件物品所需的两种代价分别为a[i]和b[i]。两种代价可付出的最大值（两种背包容量）分别为V和Q。物品的价值为v[i]。

基本思路：

费用加了一维，只需状态也加一维即可。设dp[i][j][k]表示前i件物品付出两种代价分别为m和w时可获得的最大价值。

状态转移方程就是：$f [i][j][k]=max{f[i-1][j][k],f[i-1][f-a[i]][k-b[i]]+v[i]}$。

如前述方法，可以只使用二维的数组：当每件物品只可以取一次时变量m和w采用顺序的循环。

大概就是

由一维01背包费用推广二维01背包费用还可以推广三维，四维，…..N维。

当物品有如完全背包问题时采用逆序的循环。

当物品有如多重背包问题时拆分物品。

题解-代码：


#include<iostream>
using namespace std;

const int MAX_N = 1e3;

int dp[MAX_N + 10][MAX_N + 10];

int main() {
    int V, Q, n;
    cin >> V >> Q >> n;
    for (int i = 1; i <= n; i++) {
        int m, w, v;
        cin >> m >> w >> v;
        for (int j = V; j >= m; j--) {
            for (int k = Q; k >= w; k--) {
                dp[j][k] = max(dp[j][k], dp[j - m][k - w] + v);
            }
        }
    }
    cout << dp[V][Q] << endl;
    return 0;
}

分组的背包问题

题目：

有N件物品和一个容量为S的背包。第i件物品的费用是w[i]，价值是v[i]，组别g[i]。这些物品被划分为若干组，每组中的物品互相冲突，最多选一件或者不选,如果同属于v[i]组一共有m个那最多就有m + 1种选法。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

基本思路：

$dp[i][j]$ 表前 i 组物品，能放下容量为j的背包的最大价值。

朴素算法对第 i 组物品，容量为 j 的背包，有 m + 1种选法。

$max(dp[i-1][j], dp[i - 1][j - w[1]], dp[i - 1][j - w[2]]…dp[i - 1][j - w[m]])$

这里基本就是01背包模板直接用01背包优化版的板子就可以了。

题解-代码：


#include <iostream>
#include <cstdio>
using namespace std;

const int MAX_N = 1e3;
int dp[MAX_N + 10];
int w[MAX_N + 10], v[MAX_N + 10], g[MAX_N + 10], gg[MAX_N + 10][MAX_N + 10];

int main() {
    int n, s, nn = 0;
    cin >> s >> n;
    for (int i = 1; i <= n; i++) {
        int t;
        scanf("%d%d%d", &w[i], &v[i], &t);
        nn = max(t, nn);
        g[t]++;
        gg[t][g[t]] = i;
    }
    // 枚举 nn 个组
    for (int i = 1; i <= nn; i++) {
        for (int j = s; j >= 0; j--) { // 背包容量
            for (int k = 0; k <= g[i]; k++) { // 决策
                if (j >= w[gg[i][k]])
                // 不选从 k - 1 个物品中选择一个价值最大的
                dp[j] = max(dp[j], dp[j - w[gg[i][k]]] + v[gg[i][k]]);
            }
        }
    }
    cout << dp[s] << endl;
    return 0;
}

问背包容量与决策循环是否可以调换？不能
因为更新$dp[j]$时用到$dp[i][j - w[k]]$的值，$dp[j- w[k]]$与$dp[i-1][j-w[k]]$

有依赖的背包

基本思路：

这种背包问题的物品间存在某种“依赖”的关系。也就是说，物品 i 依赖于物品 j，表示若选物品 i，则必须选物品 j。为了简化起见，我们先设没有某个物品既依赖于别的物品，又被别的物品所依赖；另外，没有某件物品同时依赖多件物品。

这个问题由 NOIP2006 中“金明的预算方案”一题扩展而来。遵从该题的提法，将不依赖于别的物品的物品称为“主件”，依赖于某主件的物品称为“附件”。由这个问题的简化条件可知所有的物品由若干主件和依赖于每个主件的一个附件集合组成。

就好比如你大一学的c\c++语言完了大二才能学数据结构，就是你不能直接学数据结构要先学完c\c++这就是依赖关系

可看上面例题

看题, 我们在选择时候会有5种情况：

选或者不选
1. 选、只选这个主件
2. 不选、直接考虑下一个
选这个主件
1. 选这个主件、并且选附件1
2. 选这个主件、并且选附件2
3. 选这个主件、并且选附件1和附件2

例题-代码：


#include <iostream>
#include <cstdio>
using namespace std;

const int MAX_N = 1e6;

int dp[MAX_N + 10];
int w[MAX_N + 10], v[MAX_N + 10], g[MAX_N + 10][3], mark[MAX_N + 10];

int main() {
    int n, s;
    scanf("%d%d", &s, &n);
    for (int i = 1; i <= n; i++) {
        int p, q;
        scanf("%d%d%d", &w[i], &p, &q);
        mark[i] = q;
        v[i] = w[i] * p;
        if (q) {
            g[q][0]++;
            g[q][g[q][0]] = i;
        }
    }

    for (int i = 1; i <= n; i++) {
        if(mark[i] != 0) continue;
        for (int j = s; j >= w[i]; j--) {
            // 1、不选 或者 只选择主件
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
            // 2、选择第一个附件
            if (j >= w[g[i][1]] + w[i] && g[i][1] != 0) {
                dp[j] = max(dp[j], dp[j - w[i] - w[g[i][1]]] + v[i] + v[g[i][1]]);
            }
            // 3、选择第二个附件
            if (j >= w[g[i][2]] + w[i] && g[i][2] != 0) {
                dp[j] = max(dp[j], dp[j - w[i] - w[g[i][2]]] + v[i] + v[g[i][2]]);
            }
            // 4、两个附件都选
            if (j >= w[g[i][1]] + w[g[i][2]] + w[i] && g[i][1] != 0 && g[i][2] != 0) {
                dp[j] = max(dp[j], dp[j - w[i] - w[g[i][1]] - w[g[i][2]]] + v[i] + v[g[i][1]]+ v[g[i][2]]);
            }
        }
    }
    cout << dp[s] << endl;
    return 0;
}

泛化物品 (了解)

定义

考虑这样一种物品，它并没有固定的费用和价值，而是它的价值随着你分配给它的费用而变化。这就是泛化物品的概念。更严格的定义之。在背包容量为 V 的背包问题中，泛化物品是一个定义域为 0 . . . V 中的整数的函数 h，当分配给它的费用为 v 时，能得到的价值就是 h(v)。这个定义有一点点抽象，另一种理解是一个泛化物品就是一个数组 h[0 . . . V ]，给它费用 v，可得到价值 h[v]。一个费用为 c 价值为 w 的物品，如果它是 01 背包中的物品，那么把它看成泛化物品，它就是除了 h(c) = w 外，其它函数值都为 0 的一个函数。如果它是完全背包中的物品，那么它可以看成这样一个函数，仅当 v 被 c 整除时有 h(v) = w · v c，其它函数值均为 0。如果它是多重背包中重复次数最多为 m 的物品，那么它对应的泛化物品的函数有 h(v) = w · v c 仅当 v 被 c 整除且 v c ≤ n，其它情况函数值均为 0。一个物品组可以看作一个泛化物品 h。对于一个 0 . . . V 中的 v，若物品组中不存在费用为 v 的物品，则 h(v) = 0，否则 h(v) 取值为所有费用为 v 的物品的最大价值。6中每个主件及其附件集合等价于一个物品组，自然也可看作一个泛化物品。