ACwin104_货仓选址

秃头王

ACwin题解

发布于：2021年3月13日

次浏览

原题链接

题目：

在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式

第一行输入整数 N。

第二行 N 个整数 A1∼ AN

输出格式

输出一个整数，表示距离之和的最小值。

数据范围

$1≤N≤1000001≤N≤100000$
$0 ≤ Ai ≤ 400000 ≤ Ai ≤ 40000$

输入样例：

1
2

4
6 2 9 1

输出样例：

解题思路:

那面如何选择中位数仓库x如果当n等于奇数那么中间的数就是中位数，如果n是偶数那么现在中间两个其实一都可以。

首先考虑在坐标轴上建立仓库$x$如图假设货仓在中间可得$|a - x| + |b - x| >= |a - b|$，$|a - x|$就是a 到 x的距离同理 $|b - x|、 |a - b|$

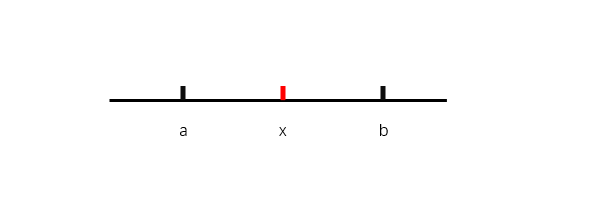
如果货仓在最左侧或者最右侧情况，那么可以看出$|x - a|$的距离就走了两遍所有放在中间才是最优解。

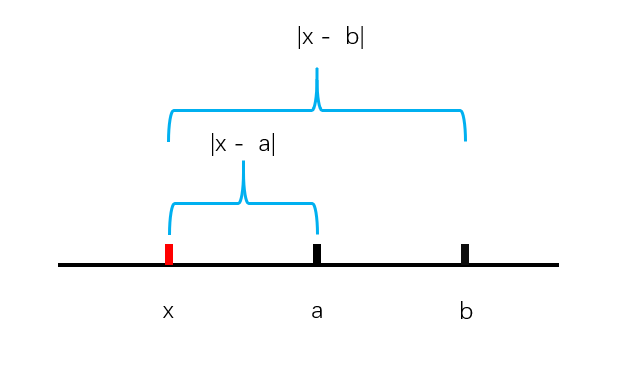
第一种做法：

#include <stdio.h>
#include <math.h>
#include <algorithm>

#define MAX_N 100000

int f[MAX_N + 10];

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", f + i);
    }
    std::sort(f, f + n);
    int res = 0;
    for (int i = 0; i < n; i++) {
        res += abs(f[i] - f[n >> 1]);
    }
    printf("%d\n", res);
    return 0;
}