抱歉，您的浏览器无法访问本站

本页面需要浏览器支持（启用）JavaScript


了解详情 >

树与二叉树

秃头王
基础数据结构

发布于：2022年1月17日
次浏览

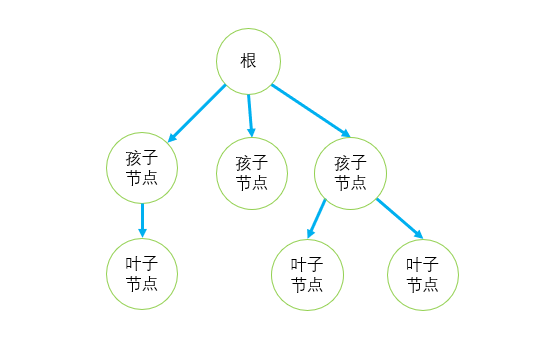
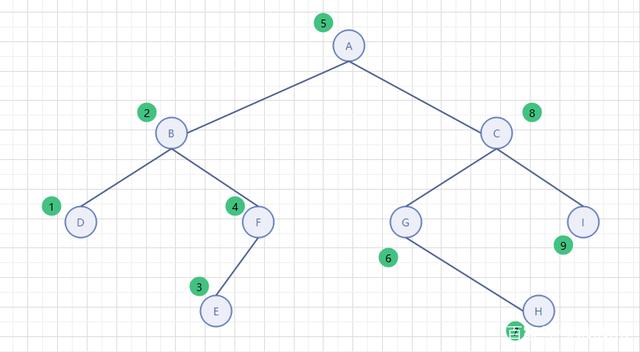
树

根节点 可以看成一个集合

链接的线可以看成关系

跟节点下面的子集

怎么判断机叉树：其中某个节点最多的子孩子个数 下面就是一个三叉树

image-20220117145202372

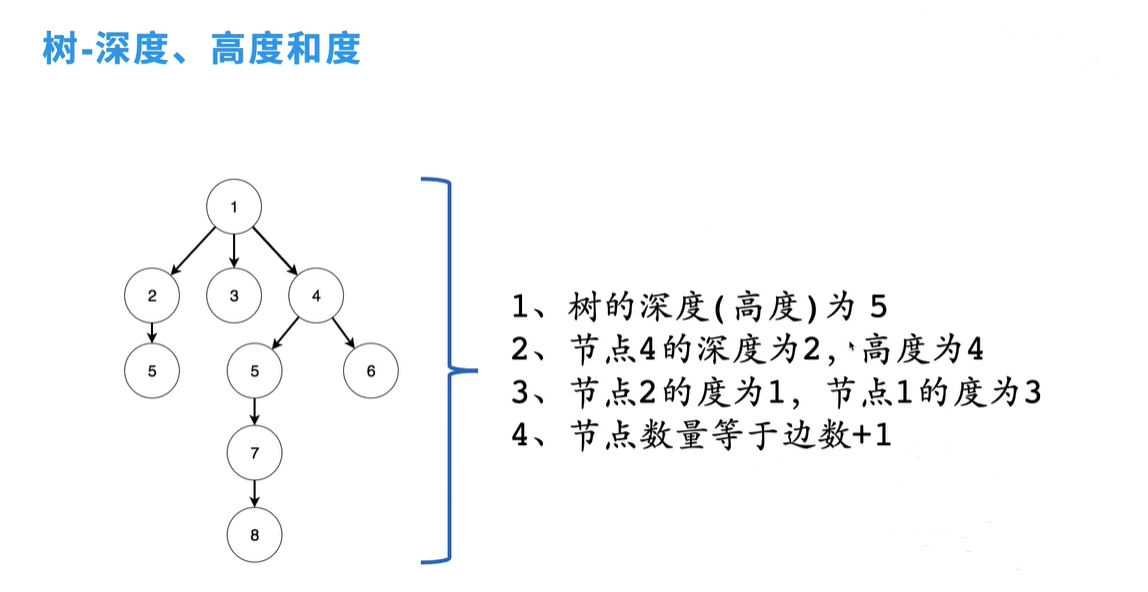
树的高度-深度

节点4深度 2 是从根节点向下看

节点4高度 4 是从节点8向上看是4 从节点6向上看是 2 取最大 4

节点4高度 分层看 也是4

什么是节点的度 数据结构的理解 度 = 出度 + 入度 图

在数据结构树的描述中 度 == 出度 从当前节点有多少条出边

节点数量等于边数+1

image-20220117145905563

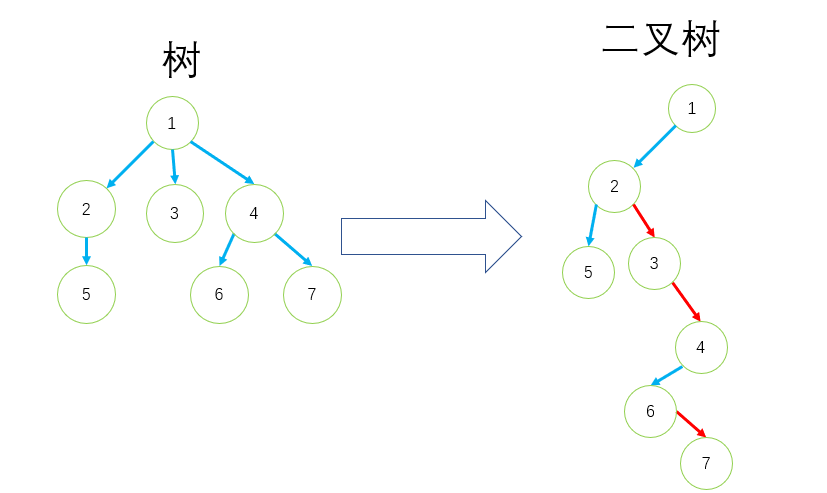
树 转 二叉树

树 转换成 二叉树 左孩子 - 右兄弟 十字链表法

image-20220117152416332

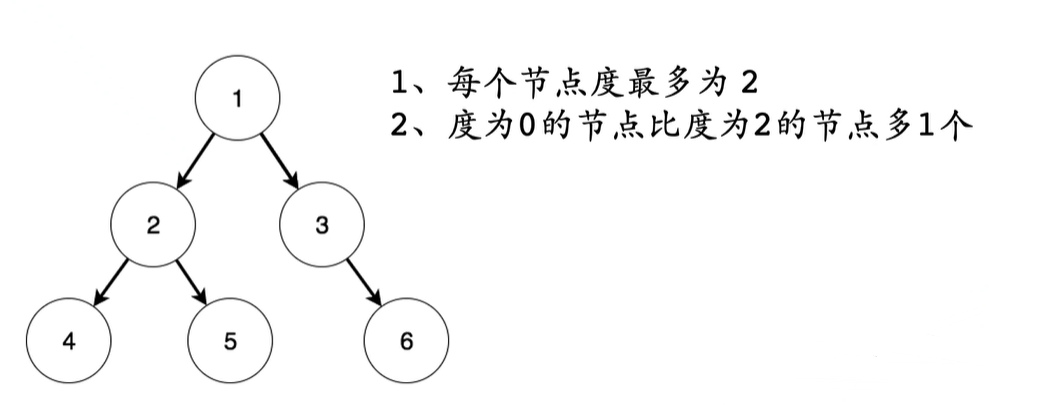
二叉树

最多有2个子孩子叫二叉树 - 度最大为2

节点1出度指向 节点 2 和 节点3 分别为 左孩子 和 右孩子

为什么要讲二叉树 因为所有的树都可以转换成2叉树

image-20220117151151131

度为0的节点比度为2的节点多1个

二叉树中 有度为0 (n0)， 1(n1)， 2(n0)

节点个数等于边数加1

n0 + n1 + n2 = 0 + n1 + 2 * n2 + 1

n0 = n2 + 1

二叉树 - 遍历

前序遍历 ： 根、左、右 — 根、左子树、右子树 ： 1， 2， 4，5，3，6

中序遍历 ： 左、根、右 — 左子树、根、右子树 ： 4，2，5，1，3，6

后序遍历 ： 左、右、根 — 左子树、右子树 、根 ：4，5，2，6，3，1

1.先序遍历- root - 左 - 右

img

1
2
3
4
5
6
void dfs(root) {
    if(root) return ;
    f.push_back(roo->val);
    dfs(root->left);
    dfs(root->right);
}

2.中序遍历 左 - root - 右

img

1
2
3
4
5
6
void dfs(root) {
    if(root) return ;
    dfs(root->left);
    f.push_back(root->val);
    dfs(root->right);
}

3.后序遍历 左 - 右 - root

img

1
2
3
4
5
6
void dfs(root) {
    if(root) return ;
    dfs(root->left);
    dfs(root->right);
    f.push_back(root->val);
}

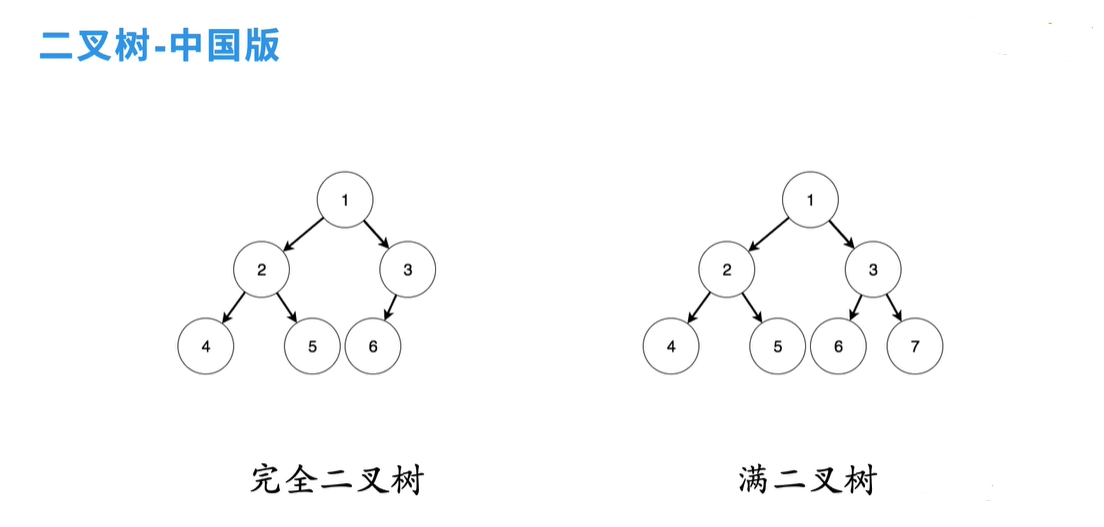
二叉树 - 中国版

完全二叉 只会有一个度为 1 的节点 缺省的只会是右孩子

满二叉树 每一个层都会满满的

image-20220117155413653

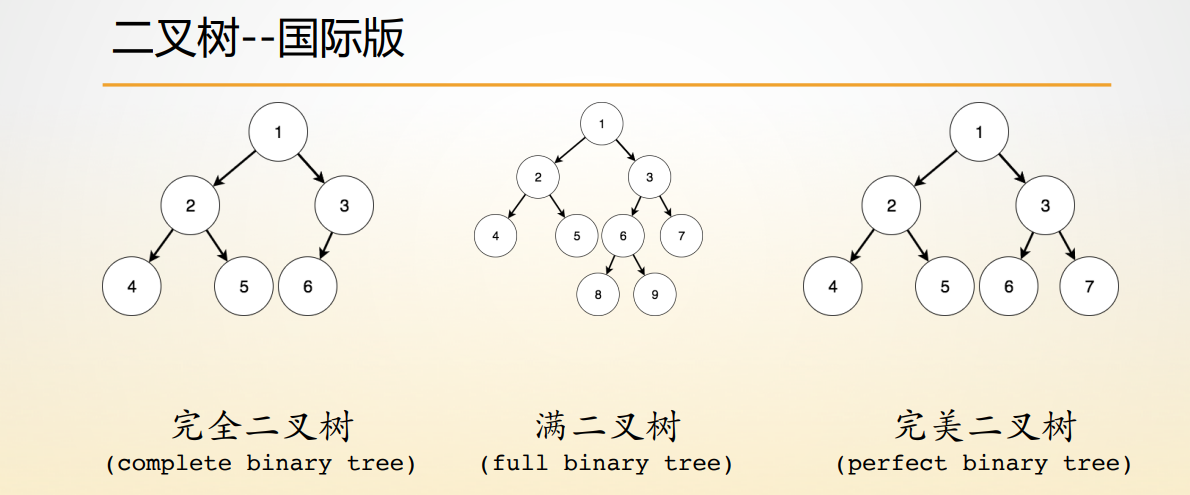
二叉树 - 国际版

image-20220117160458979

二叉树 - 完全二叉树

  1. 编号为 i 的子节点

左孩子编号 ：2 * i

右孩子编号 ： 2 * i + 1

  1. 可以用连续空间存储（数组）可以用顺序表实现！(更节省空间)

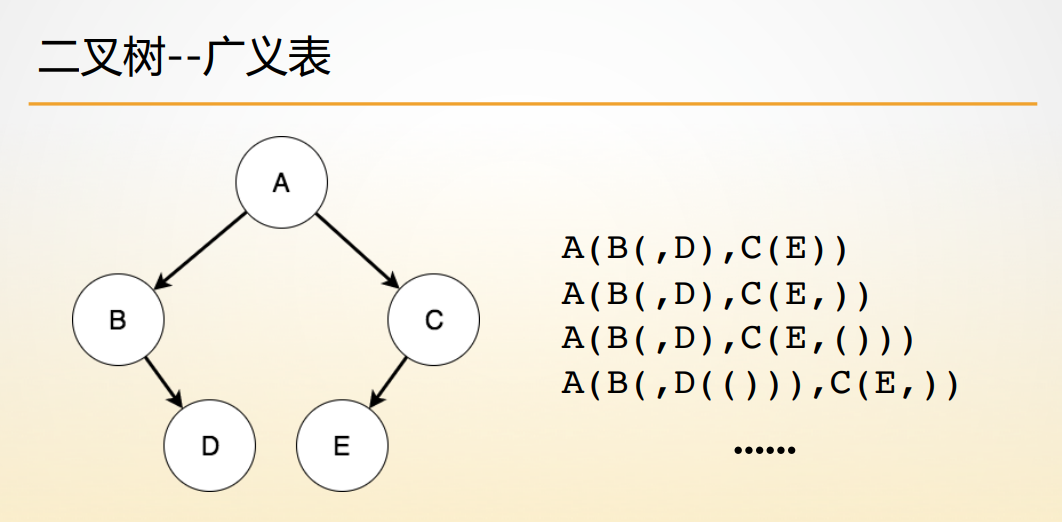
二叉树 - 广义表

广义表如何还原成一科二叉树

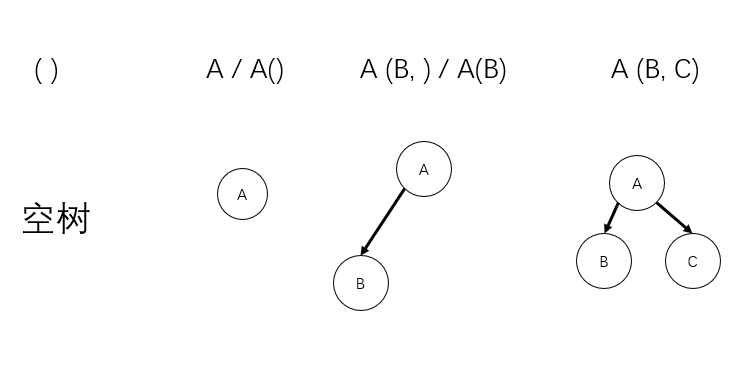
image-20220117162019366

推荐使用第一种和第二种

image-20220117162322495

二叉树代码实现

引入二叉排序树的概念

存在一课二叉树中三元组 广义表中 A, B, C

A > B && A < C (维护性质) 中序遍历就可以得到一个有序序列

前、中、后 遍历序列 得到中序和任意两种就可以还原出一课树 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
/*************************************************************************
        > File Name: 二叉树.c
        > Author: 秃头王
        > Mail: 1658339000@qq.com
        > Created Time: 2022年01月17日 星期一 16时25分06秒
 ************************************************************************/

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef struct Node {
    int data;
    struct Node *lchild, *rchild;
} Node;

typedef struct Tree {
    Node *root;
    int length;
} Tree;

Node *getNewNode(int val) {
    // 为什么使用calloc(对象数目, 每个对象大小)可以自动初始化。
    Node *p = (Node *)calloc(1, sizeof(Node));
    p->data = val;
    // 可省去
    // p->lchild = NULL;
    // p->rchild = NULL;
    return p;
}

Tree *getNewTree() {
    Tree *tree = (Tree *)malloc(sizeof(Tree));
    tree->root = NULL;
    tree->length = 0;
    return tree;
}
void clear_node(Node *root) {
    if(root == NULL) return ;
    clear_node(root->lchild);
    clear_node(root->rchild);
    free(root);
    return ;
}

void clear(Tree *tree) {
    if(tree == NULL) return ;
    clear_node(tree->root);
    free(tree);
    return ;
}
// A > B && A < C
Node *insert_node(Node *root, int val, int *falg) {
    if(root == NULL) {
        *falg = 1;
        return getNewNode(val);
    }
    if(root->data == val) return root;
    if(root->data < val) root->rchild = insert_node(root->rchild, val, falg);
    else root->lchild = insert_node(root->lchild, val,falg);
    return root;
}

// 这插入是根据二叉排序树 不会插入重复元素 falg = 标记
void insert(Tree *tree, int val) {
    if(tree == NULL) return ;
    int falg = 0;
    tree->root = insert_node(tree->root, val, &falg);
    tree->length += falg;
    return ;
}

// 前序
void pre_order_node(Node *root) {
    if(root == NULL) return ;
    printf("%d ", root->data);
    pre_order_node(root->lchild);
    pre_order_node(root->rchild);
    return ;
}

// 前序 根 左 右
void pre_order(Tree *tree) {
    if(tree == NULL) return ;
    printf("pre_order : [");
    pre_order_node(tree->root);
    printf("]\n");
    return ;
}

// 中序
void in_order_node(Node *root) {
    if(root == NULL) return ;
    in_order_node(root->lchild);
    printf("%d ", root->data);
    in_order_node(root->rchild);
    return ;
}

// 中序 左 根 右
void in_order(Tree *tree) {
    if(tree == NULL) return ;
    printf("in_order : [");
    in_order_node(tree->root);
    printf("]\n");
    return ;
}

// 后序
void post_order_node(Node *root) {
    if(root == NULL) return ;
    post_order_node(root->lchild);
    post_order_node(root->rchild);
    printf("%d ", root->data);
    return ;
}

// 后序 左 右 根
void post_order(Tree *tree) {
    if(tree == NULL) return ;
    printf("post_order : [");
    post_order_node(tree->root);
    printf("]\n");
    return ;
}

void output_node(Node *root) {
    if(root == NULL) return ;
    printf("%d ", root->data);
    if(root->lchild == NULL && root->rchild == NULL) return ;
    printf("(");
    output_node(root->lchild);
    printf(", ");
    output_node(root->rchild);
    printf(")");
    return ;
}

// 广义表打印
void output(Tree *tree) {
    if(tree == NULL) return ;
    printf("tree(%d) : ", tree->length);
    output_node(tree->root);
    return ;
}

int main() {
    srand(time(0));
    #define MAX_OP 5
    Tree *tree = getNewTree();
    for(int i = 0; i < MAX_OP; i++) {
        int val = rand() % 100;
        insert(tree, val);
        output(tree), printf("\n");
    }
    pre_order(tree);
    in_order(tree);
    post_order(tree);
    #undef MAX_OP
    clear(tree);
    return 0;
}

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://tutouwang.vercel.app/2022/01/17/%E5%9F%BA%E7%A1%80%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/%E6%A0%91%E4%B8%8E%E4%BA%8C%E5%8F%89%E6%A0%91/

更新于：2022年5月22日

树与二叉树

评论