回顾 - 二叉树
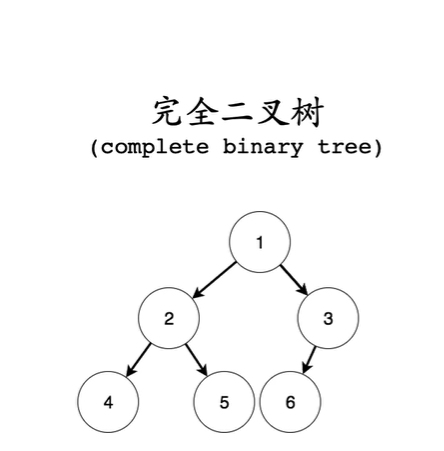
完全二叉树
- 编号为 i 的字节点
左孩子编号 :2 * i
右孩子编号 :2 * i + 1
- 可以使用连续空间存储 (数组)
堆
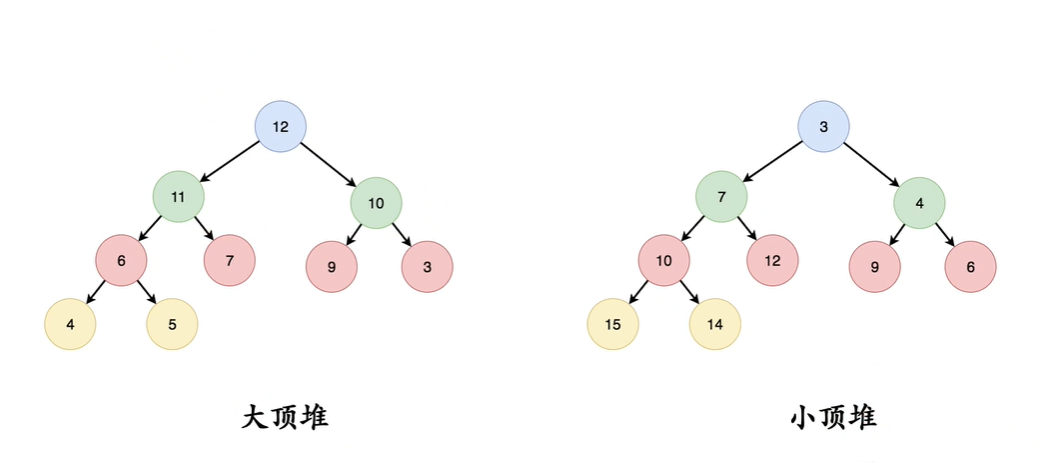
大顶堆
在任意一个三元组中 根 大于左孩子和右孩子 12 - 11 - 10 根节点 (极大) 全局最大
小顶堆
在任意一个三元组中 根 小于左孩子和右孩子 3 - 7 - 4 根节点 (极小) 全局最小
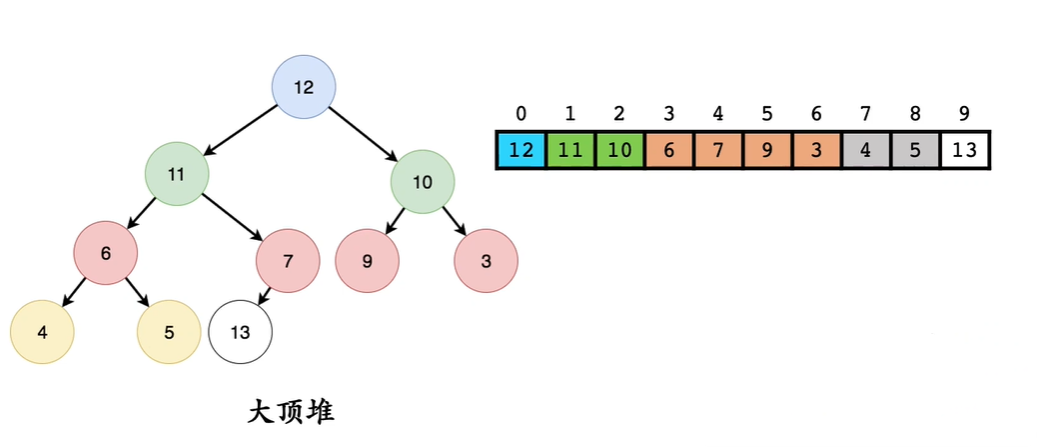
堆 - 尾部插入调整 (自下向上)
依次和和根比较
13 > 7 交换
13 > 11 交换
13 > 12 交换
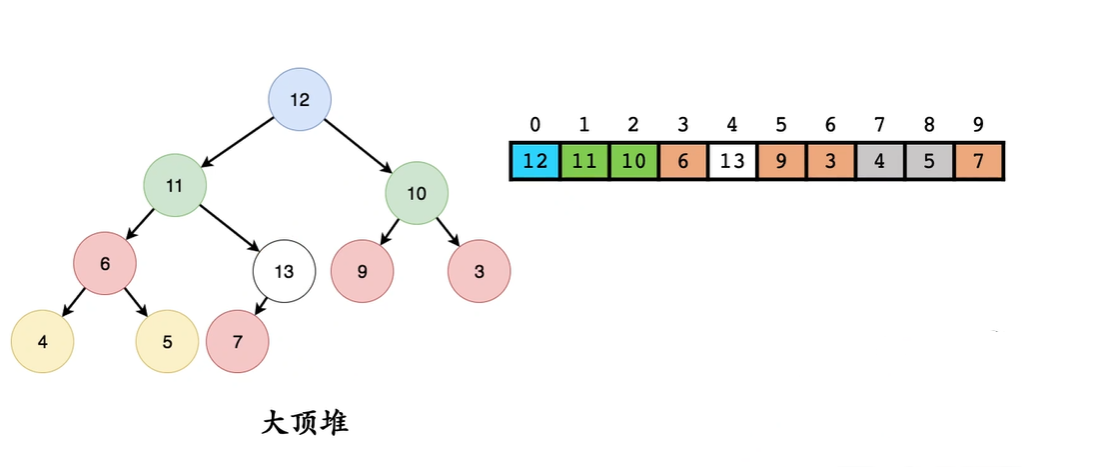
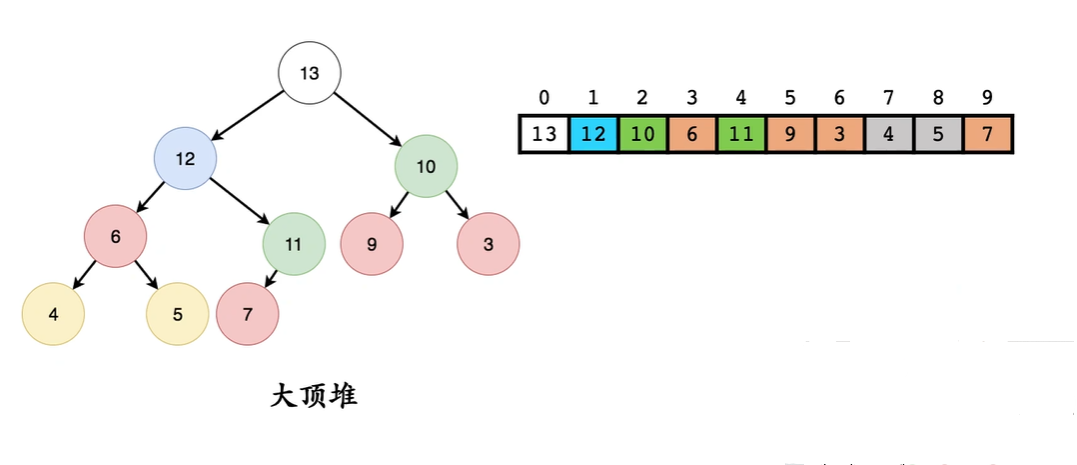
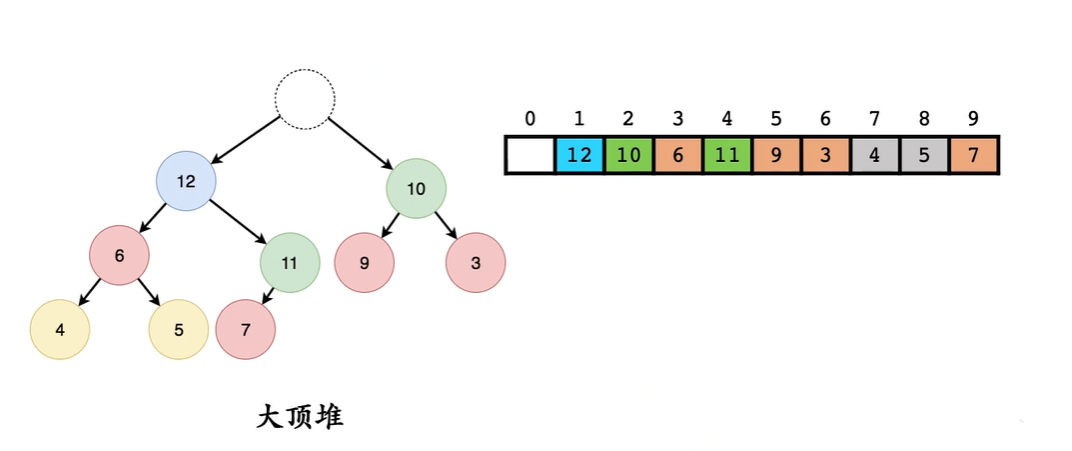
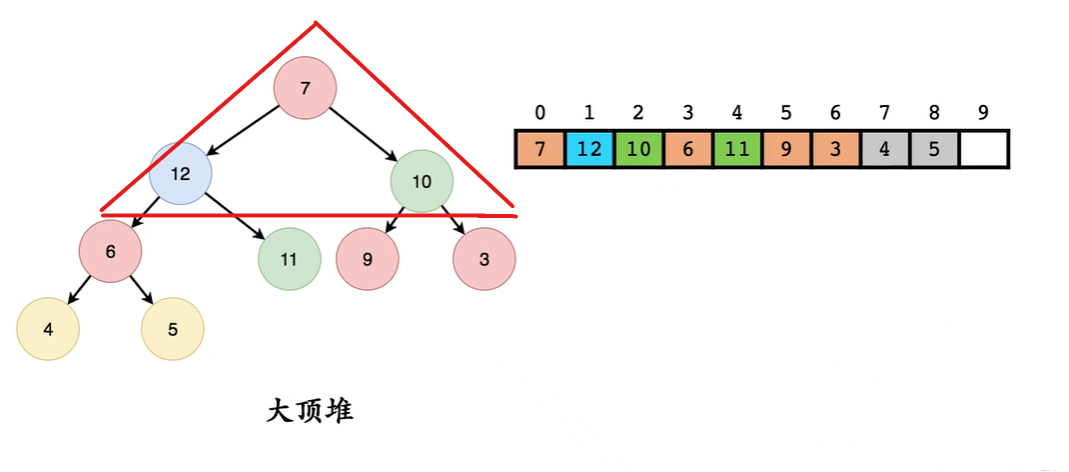
堆 - 头部弹出调整 (自上向下)
从堆的最后元素直接放到堆顶
之后在在根节点的三元组中比较是是否满足条件 如果不满足最大值和根交换一直操作
12 > 7 交换
11 > 7 交换
时间复杂度分析
插入调整时间复杂度 - 层序遍历 : $O(log^N)$
删除调整时间复杂度 $O(log^N)$
建堆时间复杂度 : $O(Nlog^N)$
堆排序 - (大顶堆情况)
口诀:
- 将堆顶元素与堆尾元素交换
- 将此操作看最做是堆顶元素弹出操作
- 按照头部弹出以后的策略调整推
如果想要一个从小到大的排序 那么就建立一个大顶堆
如果想要一个从大到小的排序 那么就建立一个小顶堆
堆 - 优先队列

堆代码实现 - (大顶堆举例)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define swap(a, b) {\
__typeof(a) __temp = a;\
a = b; b = __temp;\
}
typedef struct priority_queue {
int *data;
int cnt, size;
} priority_queue;
priority_queue *init(int n) {
priority_queue *q = (priority_queue *)malloc(sizeof(priority_queue));
q->data = (int *)malloc(sizeof(int) * n + 1);
q->size =n;
q->cnt = 0;
return q;
}
int empty(priority_queue *q) {
return q->cnt == 0;
}
int top(priority_queue *q) {
return q->data[1];
}
int push(priority_queue *q, int val) {
if(q == NULL) return 0;
if(q->cnt == q->size) return 0;
q->data[++(q->cnt)] = val;
int ind = q->cnt;
while(ind >> 1 && q->data[ind] > q->data[ind >> 1]) {
swap(q->data[ind], q->data[ind >> 1]);
ind >>= 1;
}
return 1;
}
int pop(priority_queue *q) {
if(q == NULL) return 0;
if(empty(q)) return 0;
q->data[1] = q->data[q->cnt--];
int ind = 1;
while((ind << 1) <= q->cnt) {
int temp = ind, l = ind << 1, r = ind << 1 | 1;
if(q->data[l] > q->data[temp]) temp = l;
if(r <= q->cnt && q->data[r] > q->data[temp]) temp = r;
if(ind == temp) break;
swap(q->data[ind], q->data[temp]);
ind = temp;
}
return 1;
}
void clear(priority_queue * q) {
if(q == NULL) return ;
free(q->data);
free(q);
return ;
}
int main() {
srand(time(0));
#define MAX_OP 20
priority_queue *q = init(MAX_OP);
for(int i = 0; i < MAX_OP; i++) {
int val = rand() % 100;
push(q, val);
printf("insert %d to the priority_queue!\n", val);
}
for(int i = 0; i < MAX_OP; i++) {
printf("%d ", top(q));
pop(q);
}
printf("\n");
return 0;
}
|
线性建堆法 - (自上向下)
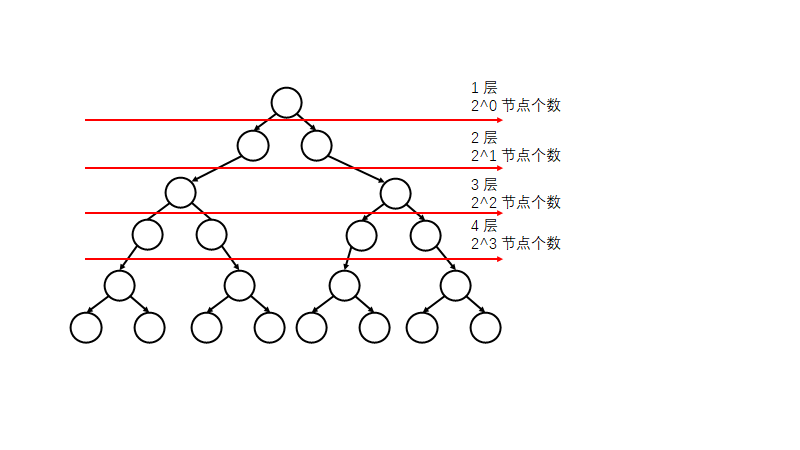
向上调整次数分析
在第 1 层时候(0表示向上调整0次) $0 * 2^0$ ($2^0$代表第一层有多少个节点)
第三次层每个节点最多向上调整2次
$0 * 2^1 + 1 * 2^1 + 2 * 2^2 + 3 + 2^3 + … + (n - 1) * 2^{n-1}$
0次 1个节点 1次 2个节点 … n - 1次 $2^{n-1}$节点
$0 * 2^{n - 1} + 1 * 2^{n - 2}$
堆排序 - 代码实现(线性建堆法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define swap(a, b) {\
__typeof(a) __temp = a;\
a = b; b = __temp;\
}
void downUpdate(int *arr, int n, int ind) {
while((ind << 1) <= n) {
int temp = ind, l = ind << 1, r = (ind << 1) + 1;
if(arr[l] < arr[temp]) temp = l;
if(r <= n && arr[r] < arr[temp]) temp = r;
if(ind == temp) break;
swap(arr[ind], arr[temp]);
ind = temp;
}
return ;
}
void heap_Sort(int *arr, int n) {
arr -= 1;
for(int i = n >> 1; i >= 1; i--) {
downUpdate(arr, n, i);
}
for(int i = n; i > 1; i--) {
swap(arr[i], arr[1]);
downUpdate(arr, i - 1, 1);
}
return ;
}
void output(int *arr, int n) {
for(int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
srand(time(0));
#define MAX_N 20
int *arr = (int *)malloc(sizeof(int) * MAX_N);
for(int i = 0; i < MAX_N; i++) {
arr[i] = rand() % 100;
}
output(arr, MAX_N);
printf("\n");
heap_Sort(arr, MAX_N);
output(arr, MAX_N);
free(arr);
#undef MAX_N
return 0;
}
|
时间复杂度分析
$O(log^N)$



















