并查集
连通性问题:
- 基于染色的思想,一开始所有点的颜色不同
- 连接两个点的操作,可以看成将一种颜色的点染成另一种颜色
- 如果两个点颜色一样,证明联通,否则不联通
- 这种方法叫做并查集的:【Quick-Find算法】
Quick-Find 近似$ O(1) $查询
Quick-Find
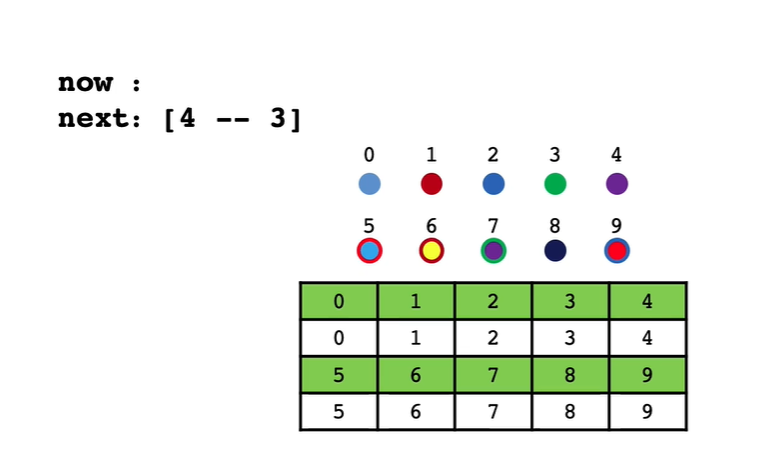
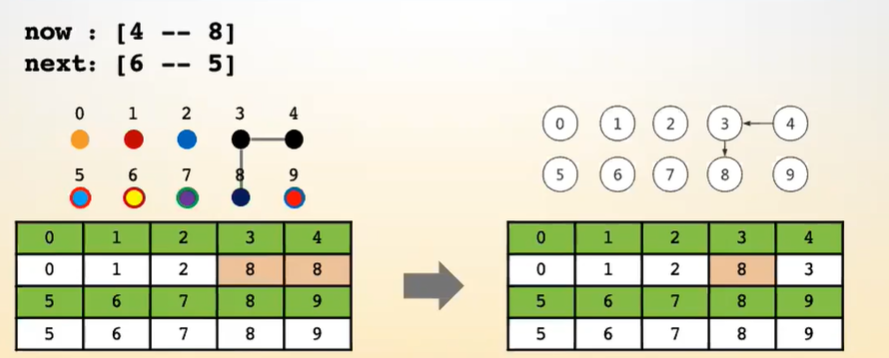
默认的做法吧前一个数字的颜色改成后一个颜色(大白话:就是让4接到3后面,让3作为根节点)
这里要说明一下 : 无论以 4 还是以 3 作为根节点都是可以的这个不重要 - 节点的链接其实是两个集合的链接
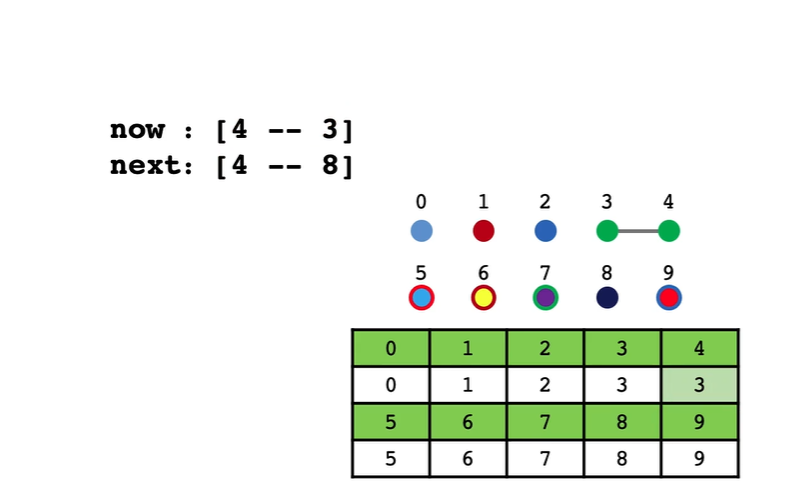
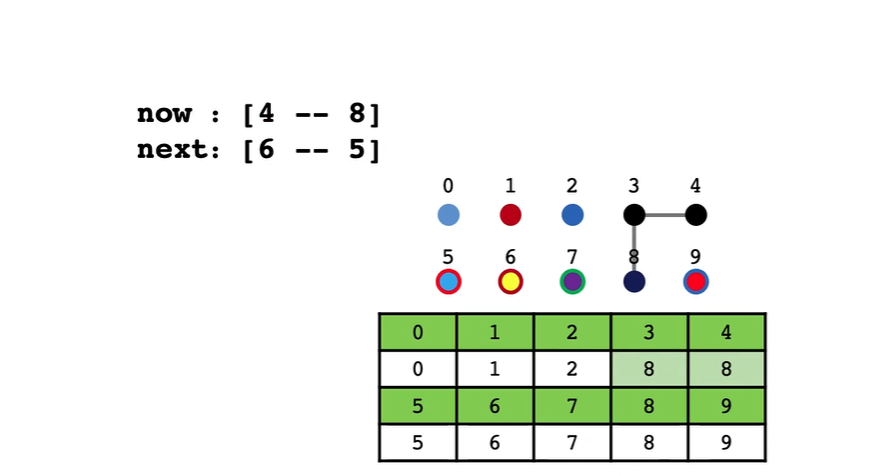
4 和 8 链接是直接吧4接到8下面么?(其实不对)
相当于 4 和 3已经属于一个集合那么你要改4当然3也要改变所以3和4的下标都要改成8
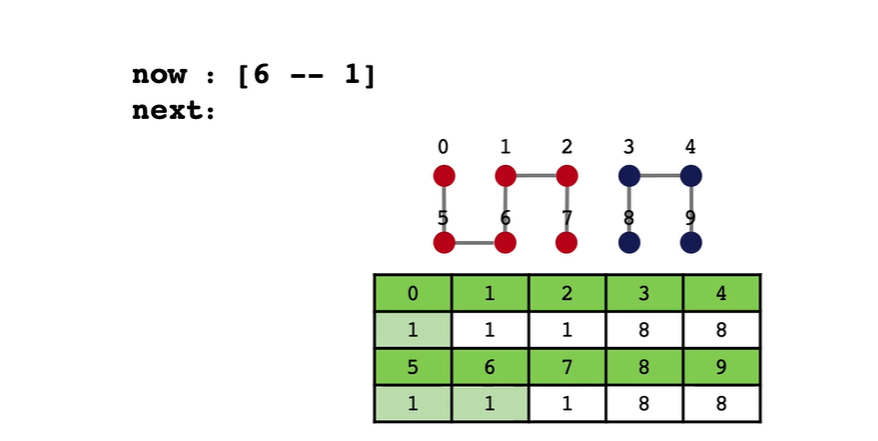
Quick-Find 时间复杂度分析
联通判断:近似$O(1)$
合并操作:$O(n)$
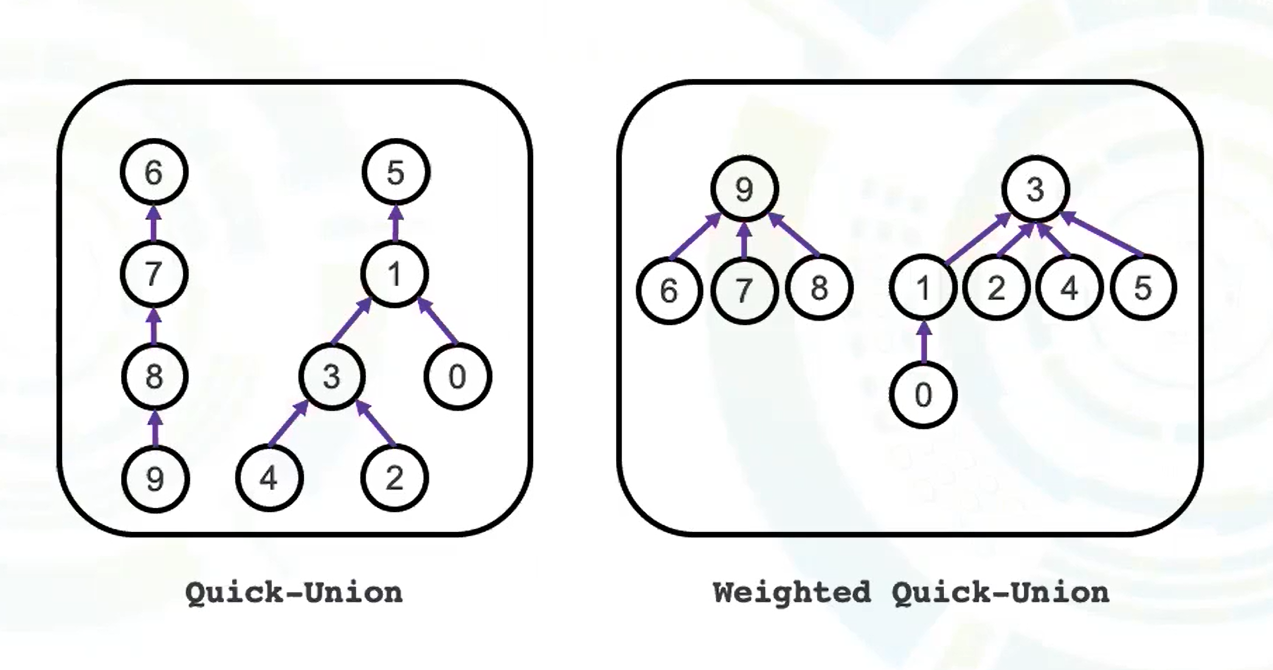
Quick-Union
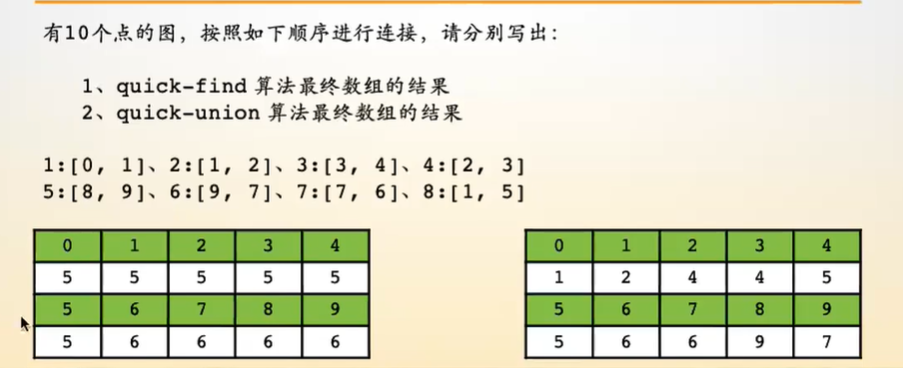
Quick-Unionu算法是选先找根节点判断是否处在同一根节点猜能在合并
Quick-Union 总结
问题思考:(需要自己手动模拟一下)

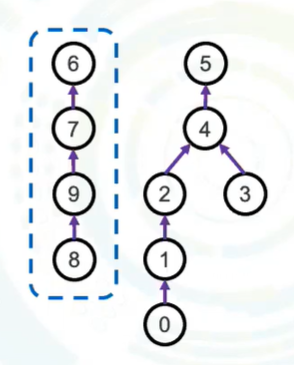
- 如果不看上述 Quick-Union 正常合并情况在极端情况下会退化成一条链 - 这就是一个$O(n)$操作
- 将节点数量多的接到少的树上面,导致了退化
- 将树高深度的接到浅的上面,导致退化
问题思考:若要改进,是按照节点数量还是节点高度合并?
可以得到:
树高合并到树矮的上面(树高不变)
如果一棵树很矮但是包含了很多节点和一颗高树有较少节点在这种情况下就需要节点数量为合并条件
平均查找次数
每个节点深度相加之和除总节点数量
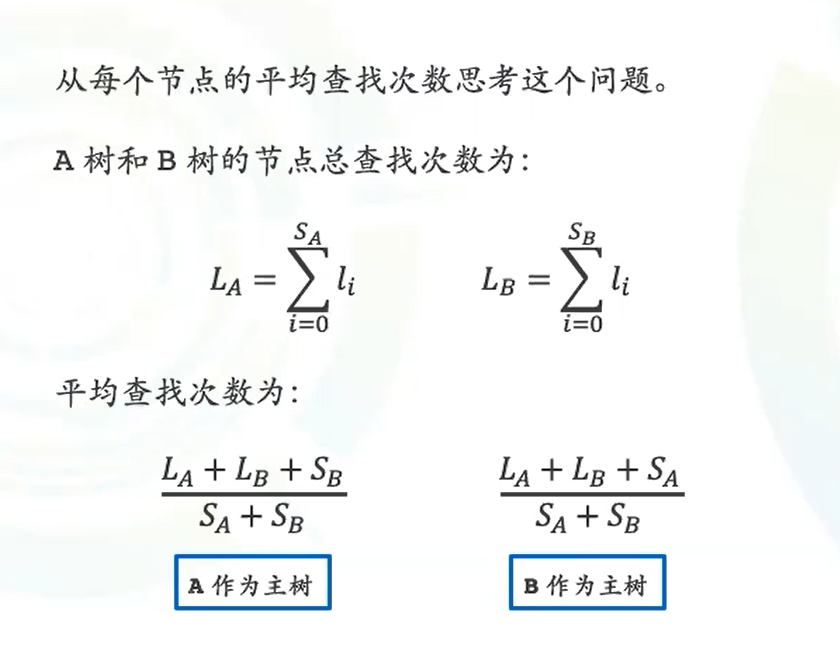
按秩合并下图 但是要把0接到3下面就路径压缩 + 按秩合并了就开头所看到的样子
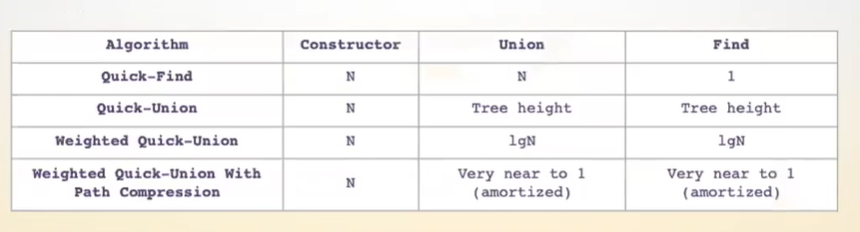
并查集四种算法
代码见 并查集2










